Công thức tính thể tích hình chóp cụt và ví dụ minh họa

Thể tích hình chóp cụt là công thức quen thuộc từ hồi trung học nhưng lâu rồi bạn không còn nhớ để áp dụng vào tính toán. Hôm nay ThuThuat123 xin chia sẻ đến bạn công thức tính thể tích hình chóp cụt và ví dụ minh họa để bạn có thể giải được các bài toán và áp dụng được trong lĩnh vực xây dựng.

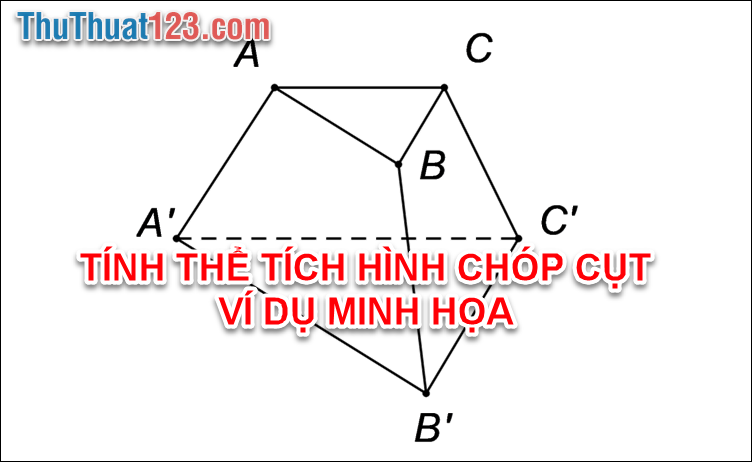
Hình chóp cụt là gì?

Hình chóp cụt là phần chóp nằm giữa đáy và thiết diện cắt bởi mặt phẳng song song với đáy hình chóp.

Tính chất của hình chóp cụt

• Hai đáy là đa giác có các cạnh tương ứng song song và tỉ số các cạnh tương ứng bằng nhau.
• Các mặt bên là những hình thang.
• Các đường thẳng chứa các cạnh bên đồng quy tại một điểm.

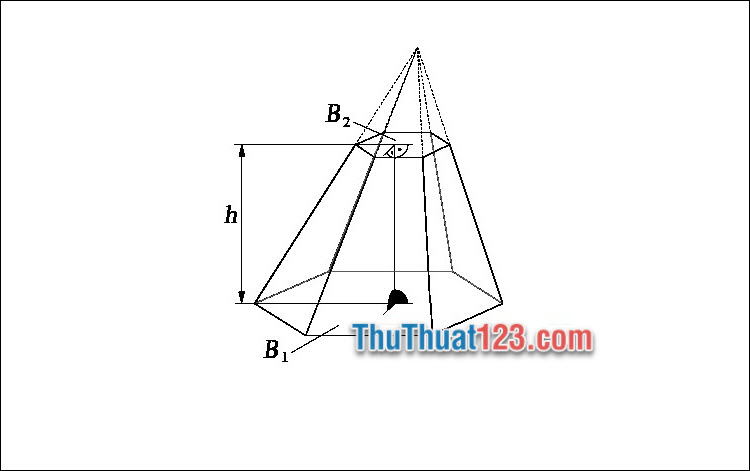
Công thức tính thể tích hình chóp cụt

\(V = \frac{h}{3}({B_1} + \sqrt {{B_1}{B_2}} + {B_2})\)

Trong đó:

• V: Thể tích hình chóp cụt
• h: Chiều cao của hình chóp cụt (khoảng cách giữa 2 mặt phẳng chứa 2 đáy)
• \({{B_1}{B_2}}\) là diện tích của đáy lớn và đáy nhỏ của hình chóp cụt.

Đơn vị thể tích được đo bằng lập phương của khoảng cách, đơn vị đo thể tích chuẩn là mét khối (\({m^3}\))

Ví dụ minh họa

Ví dụ 1: Cho hình chóp cụt tam giác ABC.A'B'C' có chiều cao h = 6 cm, tam giác ABC đều cạnh 4 cm, tam giác A'B'C' đều cạnh 2 cm. Tính thể tích hình chóp cụt ABC.A'B'C'.

Giải:

Dựa theo công thức, để tính được \({V_{ABC.A'B'C'}}\) bạn cần phải biết chiều cao, diện tích tam giác lớn, tam giác nhỏ.

Tam giác ABC đều, cạnh 4 cm nên ta có: \({B_1} = {S_{ABC}} = {4^2}\frac{{\sqrt 3 }}{4} = 4\sqrt 3 \)

Tam giác A'B'C' đều, cạnh 2 cm nên ta có: \({B_2} = {S_{A'B'C'}} = {2^2}\frac{{\sqrt 3 }}{4} = \sqrt 3 \)

Thể tích hình chóp cụt ABC.A'B'C' là: \(V = \frac{h}{3}({B_1} + \sqrt {{B_1}{B_2}} + {B_2})\)

\({V_{ABC.A'B'C'}} = \frac{6}{3}(4\sqrt 3 + \sqrt {(4\sqrt 3 )\sqrt 3 } + \sqrt 3 )\)

\({V_{ABC.A'B'C'}} = 2(4\sqrt 3 + 2\sqrt {\sqrt 3 } + \sqrt 3 ) = 14\sqrt 3 c{m^3}\)

Vậy thể tích hình chóp cụt ABC.A'B'C' là  \(14\sqrt 3 c{m^3}\)

Ví dụ 2: Tính thể tích của hình chóp cụt đều ABCD.A'B'C'D có đáy lớn là hình vuông ABCD cạnh 6cm, đáy nhỏ hình vuông A'B'C'D' cạnh 3 cm và chiều cao của hình chóp cụt là 4cm.

Giải:

Để tính được thể tích hình chóp bạn phải tính được diện tích đáy lớn, đáy bé của hình chóp cụt. Diện tích của 2 đáy lần lượt là:

\({S_{ABCD}} = 6.6 = 36(c{m^3})\)

\({S_{A'B'C'D'}} = 3.3 = 9(c{m^3})\)

Áp dụng công thức tính thể tích hình chóp cụt, ta có:

\({V_{ABCD.A'B'C'D'}} = \frac{4}{3}(36 + \sqrt {36.9} + 9) = \frac{4}{3}(36 + 18 + 9) = 84(c{m^3})\)

Ví dụ 3: Cho một hình chóp cụt đều có chiều cao bằng 3cm, đáy là lục giác đều, độ dài cạnh đáy bằng 2cm và độ dài cạnh đáy nhỏ bằng 1 cm. Tính thể tích hình chóp cụt đã cho.

Giải:

Gọi diện tích của 2 đáy hình chóp lần lượt là \({S_1}\), \({S_2}\). Khi đó diện tích 2 mặt đáy là:

\({S_1} = 6(\frac{{{2^2}\sqrt 3 }}{4}) = 6\sqrt 3 (c{m^3})\)

\({S_2} = 6(\frac{{{1^2}\sqrt 3 }}{4}) = \frac{{3\sqrt 3 }}{2}(c{m^3})\)

Áp dụng công thức tính thể tích hình chóp cụt ta được:

\(V = \frac{h}{3}({S_1} + \sqrt {{S_1}{S_2}} + {S_2}) = \frac{3}{3}(6\sqrt 3 + \sqrt {6\sqrt 3 \frac{{3\sqrt 3 }}{2}} + \frac{{3\sqrt 3 }}{2}) = \frac{{21\sqrt 3 }}{2}(c{m^3})\)

Trên đây là toàn bộ bài viết về công thức tính thể tích hình chóp cụt và ví dụ minh họa. Hy vọng qua những ví dụ trên sẽ giúp bạn hiểu hơn về công thức tính toán và áp dụng vào giải các bài tập hiệu quả nhất.