Cách tính thể tích hình trụ và ví dụ minh họa
Mục lục nội dung
Bạn đang làm bài tập mà quên mất công thức tính thể tích hình trụ? Hôm nay ThuThuat123 xin chia sẻ đến bạn Cách tính thể tích hình trụ và ví dụ minh họa, giúp các bạn nhớ lại công thức và áp dụng vào các bài toán và ứng dụng trong thực tế.

Hình trụ là gì?
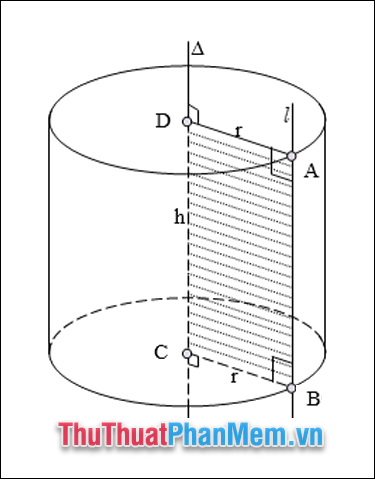
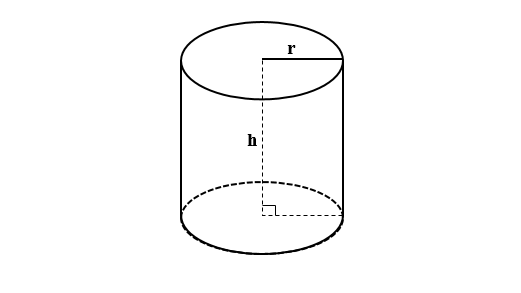
Khi quay hình chữ nhật ABCD quanh một cạnh cố định CD, ta được một hình trụ. Khi đó:
- Hai đáy là hình tròn bằng nhau và nằm trên hai mặt phẳng song song.
- DC là trục của hình trụ.
- Mỗi vị trí của AB được gọi là một đường sinh. Các đường sinh vuông góc với mặt đáy.
- AB=CD=h: chiều cao của hình trụ
- AD=BC=r: bán kính của mặt đáy
Trong thực tế, có rất nhiều đồ vật có dạng hình trụ như: lon sữa bò, chiếc cốc thủy tinh, ống nghiệm, …
Công thức và cách tính thể tích hình trụ
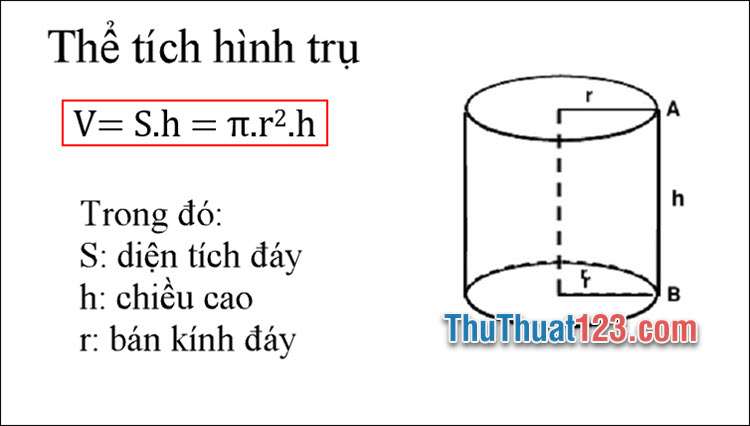
Thể tích hình trụ là lượng không gian được chiếm giữ một hình trụ nhất định.
Thể tích hình trụ bằng diện tích của mặt đáy nhân với chiều cao: V=S.h=πr2h
Trong đó:
V: thể tích
r: bán kính hình trụ
h: chiều cao
π: hằng số (π=3.14)
S: diện tích mặt đáy của hình trụ.
Thể tích hình trụ sử dụng vị đo là lập phương khoảng cách: m3, cm3
Ví dụ minh họa
Ví dụ 1: Tính thể tích hình trụ biết bán kính hai mặt đáy bằng 5cm, chiều cao hình trụ bằng 4cm.
Hướng dẫn: Em chỉ cần nhớ và áp dụng công thức tính thể tích hình trụ và thay số vào là được.
Thể tích của hình trụ là: V=πr2h=πx52x4=100π∼314(cm3)
Ví dụ 2: Tính thể tích hình trụ. Biết chu vi đáy bằng 4π (cm), chiều cao hình trụ bằng 8cm.
Hướng dẫn:
Để tính được thể tích hình trụ ta phải biết bán kính và chiều cao.
Chu vi đường tròn đáy: C=2πr⇒r=C2π=4π2π=2cm
Khi đã biết được bán kính và chiều cao ta áp dụng theo công thức:
Thể tích hình trụ: V=πr2h=πx22x8=32π∼100.48(cm3)
Ví dụ 3: Cho thể tích hình trụ là 128π, đường kính đáy của hình trụ bằng 8cm. Tính chiều cao của hình trụ?
- Từ đường kính đáy ta phải đi tìm bán kính đáy
Bán kính đáy: r=d2=82=4cm
- Để xác định được chiều cao hình trụ khi biết bán kính, ta vẫn áp dụng công thức tính thể tích hình trụ.
V=πr2h⇒h=Vπr2=128ππ42=8cm
Trên đây ThuThuat123 đã chia sẻ đến bạn công thức tính và các ví dụ cụ thể để tính thể tích hình trụ. Hy vọng các bạn có thể áp dụng được vào trong học tập và trong thực tiễn để hình học không gian không còn là nỗi ám ảnh.